Primary Directions: Behind but not Beyond the Calculations

Understanding primary directions seems formidable, particularly when one tries to grasp the spherical trigonometry that is needed to calculate such things as the RA (right ascension) or OA (oblique ascension) of a planet. If we try breaking the calculations down into their parts it becomes easier. What one is essentially doing is calculating unknown values from given values. What complicates matters is that we use two different co-ordinate systems to define the position of a planet on the celestial sphere. The first system uses the co-ordinates, right ascension and declination, with reference to 0 deg. Aries on the celestial equator. This is the position of the planet as seen from the earth. The second system uses the co-ordinates, longitude and latitude, with reference to 0 deg. Aries on the ecliptic, the Sun’s path. Then there is our position on earth, which are the familiar co-ordinates of geographic longitude and latitude.

If you look inside an ephemeris you will find that the longitudes, latitudes and declinations of the planets are given in universal time (GMT) for either midnight or noon. If you calculate a chart by hand you are basically adjusting this information for a particular time and location. The calculations done for primary directions are merely an extension of this. Here too adjustments are made for the particular time and location of a chart. The only difference is that the chart gives the reference points and the movements of the planets are adjusted to this (i.e. the positions in the chart are the Signifactors while the later positions are the Promissors).

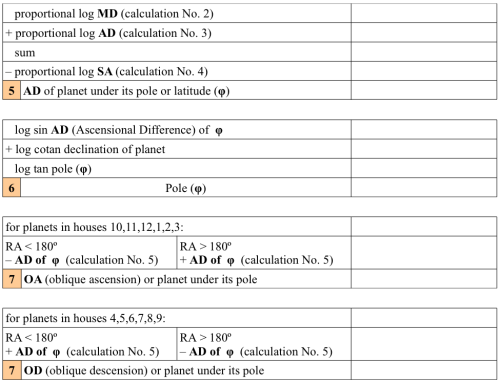
Now in order to direct a planet or other important point to any position in the natal chart we need to know what its right ascension and oblique ascension is and we may even want to consider this with reference to the exact latitude of birth.

So, how do we calculate right ascension? This is where trigonometry comes into the picture. Consider the following illustration:

It is a triangle with a right angle (C). And if we define the different points and sides of the triangle in the context of our discussion. Angle A is 23,4 degrees, the inclination of the ecliptic. This means that point A is 0 degrees Aries. Side ‘b’ is a segment of the celestial equator and side ‘c’ is a segment of the ecliptic. Point B is where a planet without latitude (such as the Sun) is located and side ‘a’ is a segment of its meridian. Side ‘a’ is therefore the declination of the planet. Side ‘b’ is its right ascension and side ‘c’ its longitude. The values that we have from our ephemeris are the declination (a) and the longitude (c), we want to discover the right ascension (b). Now the sides and angles of our triangle have a whole set of mathematical relationships that describe them. These are expressed in formulae. The formula that interests us is:

cos c = cos a cos b

We have the values ‘a’ and ‘c’ so we need to rewrite this formula:

cos b = cos c / cos a, which is:

cos of RA = cos planets longitude / cos planets declination (this can be used for a planet with 0 degrees latitude, the Sun for example)

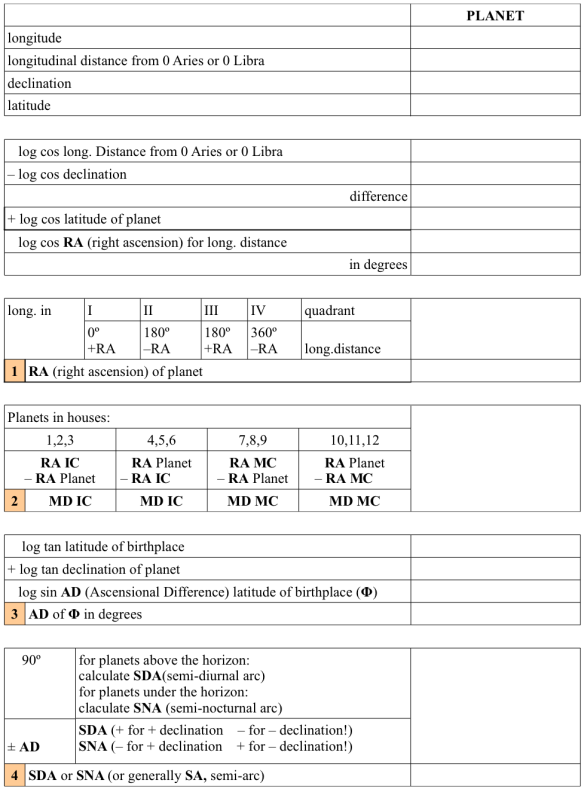
If you refer to my calculation sheet, see Calculating Primary Directions by Hand, you’ll find that this is represented by logarithms. The advantages of logarithms being that only addition and subtraction need be done instead of multiplication and division. So the formula in step 1 of the calculations is:

log cos RA = log cos longitude – log cos declination + log cos latitude.

Say our planet is at 10 Aries 00 and has a declination of 15 N 00, we would proceed by first looking up the cos logarithms for both of these values:

cos RA = 9.99335 – 9.98494 + 9.99999 (0 deg. lat) = 9.99840
RA = 4 degrees 55

From our formula we note that if the latitude of a planet is less than its declination then its RA must be smaller than its longitude. This is a check for whether our calculations are correct (not unlike checking which house the Sun is in when doing a calculation by hand. If the chart is for 11: oo in the morning there must be a mistake if it is in the 5th house!). If latitude and declination are equal then longitude and right ascension are also equal and no calculations are needed. Not that this happens often, but if one keeps an eye open it can save ten to fifteen minutes of calculation time.

What I think is really important is to understand how all of the information in the ephemeris is related to each other. If you rely entirely on your computer you may never really understand what is happening and you may not even recognise whether your software has an algorithm error.

We’ll continue looking at the calculations in a future article as I am sure this is enough to digest for the moment!

Directions for the Stout-hearted

You might ask why calculating Primary Directions by hand is necessary in the computer age. The answer is quite simple. First there is no software on the market that is affordable, easy to use and where primary directions as understood by the older astrological writers (Wm. Lilly, J.B- Morin, Joh. Schöner, Junctinius, etc.) are presented. Secondly it helps when their calculation is a little transparent and when that ideal Primary Direction programme comes along what convenience it represents!

As it is not easy to find a step-by-step calculation guide for directions I am presenting one here. This is for the stout-hearted as the calculations involve 7 steps. But if done systematically, it doesn’t take that long.

They are based on Erich Carl Kühr’s calculation example in his book, “Berechnung der Ereigniszeiten”. Erich Carl Kühr (1899-1951), is a fairly unknown German astrologer. One of his great merits, are his tables for both Right Ascension and Oblique Ascension. He was a proponent for the use of Primary Directions, and did his best to make their calculation and use as simple as possible. You will need two sets of logarithmic tables if you want to do these calculations. The first is a table of goniometric, trigonometric logarithms. The second is a table of Proportional Logarithms for 0 to 179 degrees. I have tried to find them in the internet but was not very successful. Should a reader find them I would greatly appreciate a link in the comments section to this post! (thank you in advance)

The ‘ingredients’ needed for the calculations are quite interesting:

• longitude, latitude and declination of the planets
• latitude of the birthplace

and the process:

• trigonometry
• proportion

Consider the trigonometry as a means of finding an unknown quantity (the right-ascensional arc or the oblique ascension) with known factors (longitude, latitude and declination of a planet, latitude of birthplace). It is not unlike calculating the base of a triangle given the length of the hypotenuse and the height of the side that is ‘elevated’. The trigonometric functions are merely proportional relationships to help accomplish what would otherwise be a staggering task.

Good luck!

Primary Directions: Direct!

Primary directions are easy to understand, provided one keeps in mind that their name is derived from the primary motion of the earth around its axis. If they are treated like a rarefied form of transit, which quite often is the case, then confusion is not far away.

Before there can be direction, there must be a reference from which to direct. This reference is the radical chart or the radix. The radix or root has its name for a reason. The positions of the houses and the planets remain stable, they do not change. They are rooted. This has to be deeply anchored in one’s mind.

Next, it has to be clear what is directed to what. Here two terms are used. Promittor and Significator. A Promittor, as the name indicates promises something. A Significator signifies something. So far, so good, but it is here that the authorities differ from one another as to the number of Significators and to which “moves”. Some say it is the Promittor that moves to the Significator. Others that the Significator is moved to the Promittor. As we will discover, the whole debate proves to be pointless once one understands how directions work!

The radix holds at birth pure potential. All that is contained in it is a promise for the future. This potential is not released immediately. It unfolds in the course of the life, and can be seen for example in major events that befall the native. This means that each sensitive point in the chart is a bearer of potential and so is also a Promittor. The events can then be understood as being represented by a Significator. Where are the Significators found? They are also in the chart and can also be Promittors. Again, which sensitive points should be used as Significators is a matter of debate among astrologers. Many follow Ptolomy who only allowed five; MC, Ascendant, Sun, Moon and Part of Fortune. Others argue that the natural and accidental Significators of a particular event should also be taken from the radix. For example for the Marriage of a man, Ascendant, Lord or Lady of the 7th house (accidental ruler of the wife), the Moon and Venus (natural rulers of women) should be considered. I will leave it to your discretion which Significators to use.

Now we can answer the question how the Promittors and the Significators are brought together. Quite simply through the primary motion of the earth or of the celestial sphere around the earth (both viewpoints are correct). Neither the Promittor nor the Significator moves as such. It is the earth that moves, namely through rotation about its axis. And it is this clockwise motion that directs a Promittor towards a Significator. It is this rotation, when converted to time that provides the ‘score’ for the unfolding of the life events. If you recall in the article “Priming up for Primary Directions” we discussed how the circle of the equator can be divided into 360 degrees and that each degree of longitude may also be converted to or expressed in sidereal time. You may also recall that the terrestrial sphere and the celestial sphere share the same equator, the only difference being that on the terrestrial equator each degree defines longitude and the beginning point is the meridian that passes through Greenwich while on the celestial sphere each degree defines right ascension and the beginning point is at 0 Aries. All that you have to remember is that the primary motion of the earth brings the position of the Promittor to the Significator. Imagine that the radix positions of the Promittors are all imbedded in an amber sphere and their projection to the equator is also marked. Around this sphere is a thin glass sphere on which the Significators and their projected paths to the equator are also marked. The amber sphere revolves clockwise and carries the projection of the Promittor to the projection of the Significator. The arc that is needed to bring the Promittor to the Significator is then measured. This measure is then converted into time. The rule is that each degree is also equal to one year of life. There are two conversion formulae that are used. That of Ptolomy, 1 degree = 1 year. That of Naibod, which is considered more accurate, 59 minutes 08 seconds = 1 year. As all directions are projected onto the celestial equator, the seemingly complicated (and frightening!) spherical trigonometry is merely a means for achieving this.

One thing you must not do is to treat directions like transits or secondary progressions, where the planets or other significant points are really “moved”. This is the source of most confusion, and this is where the argument begins that it is the Significator that moves to the Promittor, because the Significator is thought to move with secondary motion.

Let us look at one of the simplest directions to calculate, that to the MC. It is simple because all geographical positions that share the same longitude have the same meridian and therefore have the same right ascension. You can see this if you look in your Table of Houses. At the top of the Table usually the position of the MC for every 4 minutes of sidereal time is given along with the RAMC, the right ascension of the MC. The values for the Ascendant and houses 11, 12, 2 and 3 are then listed by latitude. There is only one value for all latitudes for the MC.

Let us say that your birthplace was 50 degrees N latitude and that the MC of your chart is at 0 Aries. Mars, Lord 10 is at 0 Gemini. Now you want to direct Mars, the Promittor, to the MC. The RAMC of Aries is also 0. The RA (right ascension) of Mars at 50N latitude is 57º 49′. This is the interval needed for the projected point of Mars on the celestial equator to reach that of the MC. This is the direction. Converted to time this would be 57 years and 10 months, if you use ptolomaic conversion or 58 years and 6 months if you use Naibod.

Happy Easter!

Priming up for Primary Directions

In the epoch of the whizz-machine one only needs to click a few buttons in a computer programme to generate a chart. This is tremendously convenient. It also has one side-effect. It is easy to forget the mathematics that underlie the chart.

A chart generally is a projection that simplifies navigation. In the case of an astrological chart it is a projection of a number of factors combined to give the best possible overview. It can in a sense be described as a planetary seal whose very 2-dimensionality provides a window to grasping both a complex astronomical as well as metaphysical reality. It is a navigation tool.

What is it a projection of? Here we need to look closer at the three-dimensional reality and must resort to spherical geometry. Have no fear! I am not going to present the theoretical geometry. Instead I will try to help you envision the geometry.

Place before your minds eye a transparent sphere. This sphere will represent the earth. Next imagine that this sphere is divided into two equal halves by a circular section. The section is the equator and the halves are the north and south hemisphere.

Next imagine another circular section that is perpendicular to the first. This section divides the sphere into an eastern and western hemisphere going thorough its north and south poles. Let us say that this particular section bisects a point that has been established, by convention, to be the starting point of 360 sections that equally bisect our imagined equator. This is the meridian that passes through Greenwich, England. All 360 equal sections are also called degrees of longitude. You still awake? Yes? See, it’s easy!

But what if we want to exactly pinpoint the position of Greenwich, which is a little more than halfway the distance from the equator to the North Pole? Here we have to imagine 90 increasingly smaller sections that are parallel to the equator. These are degrees of latitude. And so we can exactly define the position of any place on earth, not only Greenwich, (51N28 latitude, 0E00 longitude), with two coordinates. I won’t go into detail here, but the parallel of latitude also helps define the horizon.

But we are not finished yet. Let us take another position east of Greenwich, say Berlin which is roughly 13 degrees east of Greenwich and 52 degrees north of the equator. But why do we used the term degrees? Well, the distance from Berlin, let us call it point B, along the same meridian, to a point on the equator, let us call it E, is the arm of an angle that runs from B to the centre point of the earth and from there to point E. (Point E can be said to be a projection of point B onto the equator) This is a 52 degree angle. The 13 degrees of latitude longitude are also an angle between the projection of B on the equator and the projection of Greenwich to the equator. You can see here that our reference is always to the equator. This is important because this same principle is used elsewhere. We’ll get to that later.

Now these 360 degrees are special because they can also be converted to time. How’s that possible? Well if we imagine that our imaginary sphere rotates around its axis in one day then we can divide the 24 hours for one revolution into equal divisions of time. There is just one tiny catch, when applied to the earth the revolution is 4 minutes shorter than clock time. We speak of a sidereal time to make just that distinction. If you are calculating a chart the old-fashioned way, this will be one of the first conversions you will make. From clock time to sidereal time. This revolution of the earth around its axis in one day is also called primary movement and it is reflected in our chart by the houses, whose movement is also clockwise. Primary movement is also what underlies what is known as primary directions. (I’ll discuss these in a followup article). Up to here, with the aid of a Table of Houses we have the first set of calculations needed for our chart. We have an empty chart with the house divisions.

Now there are two other spheres that we consider in our calculations. These are the celestial sphere and also a sphere whose “equator” is formed by the path of the Sun in its yearly revolution around the earth. This is the ecliptic. The ecliptic is not divided into 24 hours but into 12 Celestial Signs of 30 degrees each. The beginning point for both the ecliptic and the celestial sphere is where the ecliptic crosses the celestial equator at 0 degrees Aries.

The celestial sphere shares the same equator as the terrestrial sphere. But instead of describing the position of a planet on the celestial sphere in terms of longitude and latitude we speak of right ascension and declination. The angle of projection of a planetary body to the celestial equator is the Declination. The angle on the celestial equator formed by this projected point to 0 degrees Aries is known as Right Ascension.

And now to the ecliptic. This can be considered as the equator of a sphere that is tilted roughly 23 degrees away from the terrestrial and celestial spheres. Now a planet’s position can also be defined in terms of the ecliptic. Here again we speak of a planet’s longitude and latitude. This is the second set of calculations needed to cast a chart. This is done with the aid of an ephemeris. This second set of calculations are for the secondary movement of the planets which is counter clockwise. Secondary Progressions are based on this movement of the planets. That is in fact the origin of the names for Primary Directions and Secondary Progressions.

There is just one last point to be made. When we calculate our planetary positions and place them in the chart, we reduce their three dimensional position to two dimensions. When I say a planet or a fixed star is at 29 degrees Leo I have projected its real position to the ecliptic. For example we read in our ephemeris that Mars and Jupiter are conjunct at 27 Gemini. If the sky is clear, and both planets do not have the same degree of latitude we will see that one is above the other. Astrologically we say that the planet with the higher latitude is stronger. What we are saying is that when we project their position in the celestial sphere to the ecliptic they both share the same ecliptic point.

Dear reader. If you could follow all of this then you should have no difficulty in understanding primary directions in particular and I haven’t mentioned such creatures as sin., cos., tan., cot., semi- diurnal or nocturnal arcs until now”! 🙂 You have been primed! You see the general confusion about directions is such that even most programmer’s of astrological software get them wrong and should the rare programmer get them right they are presented in an unusable form!*

*If you are a purveyor of astrological software please do not solicit your software here. You may of course send me a message in the “Reply” section provided at the bottom of the home page. If you are convinced that you have the primary directions programme then you may certainly send me a usuable demo version! 🙂 or :-(?